Conceitos básicos de redes neurais: Um guia visual e interativo

Motivação

Não sou um especialista em machine learning. Sou engenheiro de software por formação e tive pouca interação com IA. Sempre quis me aprofundar no Machine Learning, mas nunca encontrei o meu lugar. É por isso que quando o Google abriu o código-fonte do TensorFlow, em novembro de 2015, fiquei super animado e sabia que era hora de começar a jornada de aprendizado.

Não quero parecer dramático, mas pra mim foi como se Prometeu entregasse o fogo do Monte Olimpo do machine learning à humanidade. Eu sempre acreditei que toda a área de Big Data e a evolução de tecnologias como o Hadoop aceleram muito mais rapidamente quando os pesquisadores do Google publicaram o paper de Map Reduce. Só que dessa vez não foi apenas um artigo, foi um software usado internamente depois de anos e anos de evolução.

Então comecei a aprender o que dava sobre o básico do assunto e vi a necessidade de um material mais simples para pessoas sem experiência na área. Esta é minha tentativa nisso.

Começando devagar

Vamos começar com um exemplo simples. Digamos que você esteja ajudando uma amiga que quer comprar uma casa. Ela achou um valor de R$ 400.000 por uma casa de 2.000 metros quadrados. Este é um bom preço ou não? Não é fácil dizer sem uma referência. Então você pergunta a seus amigos que compraram casas na mesma região e monta essa tabela:

Área (m²)	Preço (R$)
2.104	399.900
1.600	329.900
2.400	369.000

Pessoalmente, minha primeira tentativa pra chegar em algum lugar seria obter o preço médio por metro quadrado. Neste caso, isso equivale a R$ 180 por metro quadrado. (pode ser que você usasse outra abordagem, mas foque apenas no cálculo por agora)

Bem-vindo à sua primeira rede neural!
Ainda não estamos no nível do ChatGPT, mas agora você conhece a ideia fundamental por trás.
Nós podemos representar essa rede neural assim:

Diagramas como este mostram a estrutura da rede e como ela calcula uma previsão:

• O cálculo começa no círculo roxo, onde está escrito Entrada (x) . Chamamos ele de “nó de entrada” (input node). É o valor que vamos fornecer.
• O valor de entrada flui para a direita, seguindo a seta.
• Então, ele passa por um processamento, ali no círculo verde, que é apenas uma simples multiplicação pelo 180 que descobrimos. Chamamos isso de peso (em inglês: Weight).
• E , por fim, o resultado se torna nossa saída (o y, representado pelo círculo rosa).
• Isso também é chamado de “modelo matemático”, ou, para os íntimos, apenas “modelo”, pois repare que é igual uma função mesmo( y = algumacoisa)

No nosso exemplo de ajuda da sua amiga, o preço “ideal” pros 2000 m², segundo nossa rede neural seria: 2000 x 180 = R$ 360.000
E pronto, agora é comparar e dizer para sua amiga que o preço que ela achou (os 400 mil, está acima da média).

Nesse ponto, foi tudo simples assim mesmo: calculamos uma predição através de uma simples multiplicação.
O desafio mesmo foi descobrir o valor pelo qual multiplicar, isto é, descobrir o peso. E para isso, usamos uma simples conta de média. Depois, nós veremos algoritmos melhores que podem ser usados à medida que temos mais dados de entrada e modelos mais complexos.

Encontrar este valor de peso é o que chamamos de treinamento. Portanto, sempre que você ouvir falar de alguém treinando uma rede neural, isso significa apenas encontrar os pesos que usamos para calcular um valor final (“valor final” tem vários nomes nesse mundo: resultado, predição, inferência, etc.).

A imagem abaixo demonstra o mesmo modelo acima, porém em forma de função matemática. Este é um modelo preditivo simples que recebe uma entrada (X), faz um cálculo e fornece uma saída (y). Como a saída pode ser qualquer valor (0,2, 0.000001, 1000.0222, etc.), que chamamos de valores contínuos, o nome técnico dele é modelo de regressão. (mas isso é só uma curiosidade, não faz diferença saber disso agora).

y = W x

Visualmente é mais fácil de entender… Por isso, vamos tentar visualizar estes dados que temos em um gráfico.
Para que os números não fiquem gigantes no gráfico, vamos mudar nossa unidade de preço para R$ 1.000. Por exemplo, o valor de R$ 399.900, vai ser mostrado como 399 apenas.
E por conta disso, pra manter a mesma proporção, a função y = 180x, vai ficar y = 0,180x:

Melhorando o resultado

Podemos fazer melhor do que estimar o preço com base na média dos nossos dados? Vamos tentar. Primeiro, vamos definir o que significa ser melhor neste contexto.
Se pegássemos aqueles dados de referência (áreas e preços que levantamos com os amigos), e aplicarmos o nosso modelo, o quão bom ele seria?
Isto é, vamos pegar cada ponto original que temos e multiplicar pelo 0,180 e vamos ver onde os pontos calculados ficarão no gráfico:

É muito amarelo ali no final do gráfico, hein!? E amarelo aqui não é bom… Significa erro!
Quando falamos de rede neural e treinamento, queremos diminuir ao máximo esse amarelo, isso é: queremos diminuir o erro!

Pra entender melhor o conceito do erro, vamos, primeiro, montar uma tabela:

Área (x)	Preço (y_)	Predição (y)	y_ – y	(y_ – y)²
2.104	399,9	379¹	21	449
1.600	329,9	288	42	1756
2.400	369	432	-63	3969
		Média:		2.058

Vamos explicá-la por partes:

1. A coluna Preço contém aquele preço que pegamos com os nossos amigos (nossos dados de referência). Chamamos ela de  y_ pois é o resultado real que temos (um preço real e não o resultado do nosso modelo).
2. A coluna Predição (que chamamos de y) é o valor que obtivemos aplicando a função y = 0.180x
   ¹ na primeira linha, o resultado é na verdade é 378,72, mas por simplicidade, arredondei para 379
3. Como o objetivo é achar um modelo (função) que acerte o mais próximo possível do real, nós precisamos calcular a diferença entre o resultado real (y_) e o resultado da função (y).
   Essa diferença, nos dá o quanto esse valor calculado está longe ou perto do valor real. Nosso objetivo é que essa diferença seja o mais próximo possível de zero ,ou seja, quanto mais próximo de zero significa que o resultado tá sendo quase que igual ao real.
   Por isso, geramos a coluna y_ – y. Ela é apenas essa diferença entre o real e o calculado.
4. Então, nós podemos fazer uma média desses valores para ter um valor só que nos diga o quanto de erro nossa função gerou.
   Se essa média for 0, significa que cada diferença foi 0, então nosso modelo não errou… Ou seja, quanto mais próximo de zero, melhor ele está sendo.
   Mas tem um pequeno problema…
5. Repare que uma das diferenças, é negativa: -63.
   Nesse contexto, não podemos somar valores negativos com positivos, pois eles podem se cancelar: imagina se as outras duas diferenças anteriores fossem 30 e 33, o que daria 63.
   Aí, quando somasse com -63 da última, a média daria 0. Isso nos levaria a falsa sensação de que nosso modelo chegou no melhor resultado, mas estaríamos enganados!
   Para evitar isso, precisamos tirar o negativo… E uma das maneiras de se fazer isso é elevando ao quadrado: qualquer número elevado ao quadrado sempre resulta um número positivo (há outras formas também, escolhemos essa e as razões não são importantes agora).
   Por isso, criamos a coluna (y_ – y)². Ela é apenas aquela diferença elevada ao quadrado. Com isso, sempre teremos um erro com sinal positivo, e nossa média não irá nos enganar!
6. E agora que temos um número sempre positivo, podemos fazer a média dele: No caso acima, é (449 + 1756 + 3969)/3 = 2.058

Agora temos uma definição do que é “ser melhor”: um modelo melhor é aquele que resulta em menos erros. E temos um erro total, que é a média dos errinhos de cada ponto. Isso é chamado de Erro Quadrático Médio (Wikipédia) (em inglês: Mean Square Error, ou MSE). E também, nesse contexto de treinamento do nosso modelo, ela se torna o que é chamado de função de perda (loss function) ou função de custo (cost function).

Agora que temos uma forma de medir quando o modelo está melhor ou pior, vamos tentar mudar o valor do peso e ver como isso afeta o erro:

Agora que incluímos uma soma na nossa reta, ela consegue se aproximar muito mais dos nossos valores de referência. Esse valor é chamado de “viés” (bias, em inglês).
Aquele diagrama da nossa rede neural, agora fica assim:

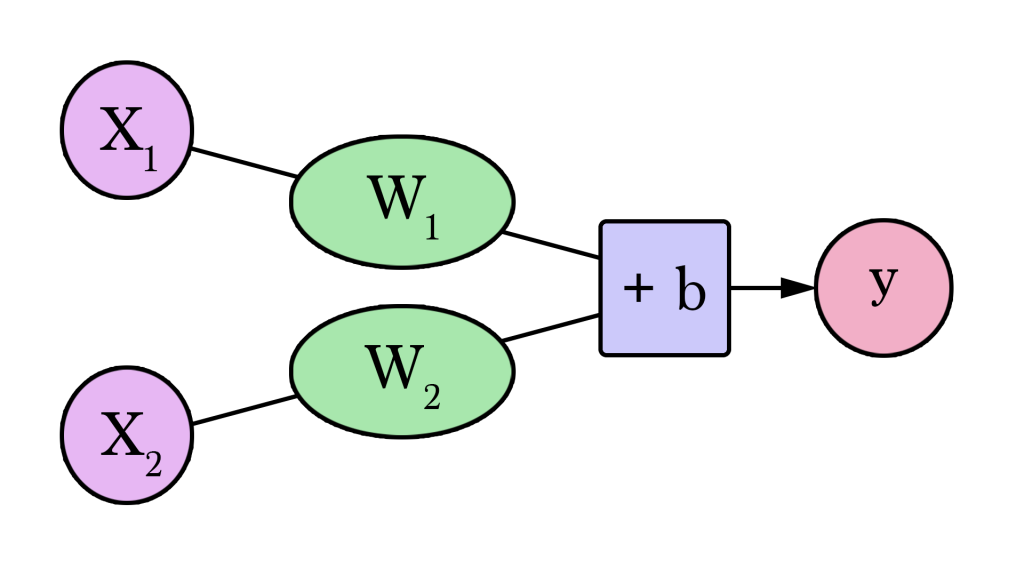
A versão genérica dessa rede neural, com com uma entrada e uma saída (spoiler: sem camadas ocultas) seria assim:

Neste diagrama, W e b são valores que encontramos durante o processo de treinamento.
X é a entrada que inserimos na fórmula (no nosso exemplo, a área). E o Y é o preço estimado (a saída da nossa rede).
E, a versão matemática dessa rede neural, isto é, a função que representa ela é:

y = W x + b

Substituindo os W e o b, ficaria assim:

y = 0.100 x + 150

Treine seu dragão

O melhor pra aprender é na prática! Tente você mesmo treinar nossa rede neural para descobrir o melhor valor para W e b, isto é, o valor que causa o menor erro possível.

Automatizando o treino

Parabéns por treinar manualmente sua primeira rede neural!!! Agora, vamos ver como podemos automatizar esse processo de treinamento. Abaixo, temos outra simulação, agora com uma espécie de “piloto automático”. São os botões “GD”. Esses botões ativam um algoritmo chamado Gradiente Descendente (Gradient Descendent) que tentam ir ajustando os valores do peso (weight) e do viés (bias) até achar os que produzem o menor erro. Cada botão contém um número que indica o quanto de etapas ele vai executar cada vez ativado. Quanto mais etapas, mais rápido ele chega no resultado. Por exemplo, o botão GD 1 executa apenas 1 etapa, enquanto que o botão GD 10 executa 10 vezes.

Os dois novos gráficos servem para ajudá-lo a rastrear os valores de erro enquanto você mexe nos parâmetros (W e b) do modelo. É importante acompanhar o erro, pois o processo de treinamento visa reduzir esse erro tanto quanto possível. Com esses gráficos você consegue ir vendo em quais valores de W e b seu erro diminui…

Como o Gradiente Descendente sabe como ajustar os valores? Disciplina de Cálculo. Aqui é onde as temidas derivadas são usadas. O objetivo do post aqui é ser bem simples, e por isso não vou entrar muito no detalhe disso para não confundir. Mas o que você precisa saber é: Através das derivadas, é possível saber o quanto temos que aumentar ou diminuir W e b de forma a reduzir o erro para o menor valor possível! É uma coisa linda de se ver!

---

E vamos parando por aqui! O artigo original continua! Mas para manter o conteúdo simples e permitir você revisar com calma, eu vou deixar o restante para uma segunda parte!
Fica ligado no blog, que em breve posto o restante!

E aí, o que achou? Teve alguma dúvida, alguma coisa não funcionou? Fica a vontade para deixar o comentário!!!